不変則批判
[不変則の紹介]
[不変則批判]
[不変則批判再論]
[対判定擁護]
←[パターン認識雑論]
←[中野の研究紹介]
←[中野の目次]
経緯
本資料は、1997年頃あるところで展開された議論の参考として執筆したものである。
残念ながら、この資料をどこかの学会誌に投稿しても採録はされないだろう。
しかし、消えるには惜しい内容と考えるので、自分のページで紹介することにした。
見直しているうちに、議論の不十分なところに気付いたので、
不変則批判再論にまとめる。
本文は再論にいたる思考過程を述べたものである。
1 序論
議論のきっかけは、
安田氏によるパターン認識における不変則である。
参考資料としては [1] がある。
以下、この資料で提案された規則を「不変則」、その中の式 (3)の性質を「安定性」と略称する。
また、資料全体で展開されている理論を「安田理論」と呼ぶ。
2 パターン認識について
2.1 パターン認識の定義
議論を簡単にするために、パターン認識の定義を [1] に書かれているものとしよう。
2.2 パターン認識の構成要素
あるパターン認識方式を論ずるとき、
それが次の二つからなっていることに留意しなくてはならない。
- 認識手法 (認識アルゴリズム)
- 標準パターン (辞書)
学習とは、標準パターン(辞書)の設定方法と言い替えることができる。
誤解のないように言っておくと、標準パターンは、
整合法に限らず、任意の認識方式に存在するものであるが、
この説明は[パターン認識雑論]の中の
「標準パターンとは何か」に譲る。
認識アルゴリズムと辞書とは完全には分離できない。
普通は、特徴抽出の改良や各種パラメータの修正はアルゴリズムの中に含めて考える。
しかし、これらの改良は誤読パターンを見て、それに対する対策として行うものであるから、
広義の学習と考えることもできる。
本小論では、このような特徴抽出の改良やパラメータ修正も学習として考えることにするが、
その立場でも以下の所論は成立する。
2.3 パターン認識手法か辞書作成法か
安田理論は、認識手法(アルゴリズム)の良否を論じているのか、
学習方法(辞書作成法)の良否を論じているのか判然としない。
筆者の理解では、不変則とは学習方法が満たすべき条件と考える。
次の疑問は、学習途中の性質の議論なのか、学習が完成して作られた辞書の議論であるのかが、
また判然としない。筆者は、学習途中の性質はどうでも良く、
学習が完成したときの性格を論ずれば良いと考える。
安田理論を見直したら、安田氏は仮定2.で
2.学習は、iについて逐次的に行われるものとする (i はクラス番号)
と書いている。
したがって、「不変則」とは学習が完成して作られた辞書の性質について論じている。
しかし、論文を読んで識別方式の良否を論じているかのごとく誤解する人は多いのではないか。
3 不変則は本当に成立するか
3.1 安定性の妥当性
本当に、安定性が正しい基準かどうかは別にして、取り敢えず正しいものと仮定する。
3.2 クラス固定
まず、認識対象クラスは増えないものとしよう。話の都合上、数字とする。
この場合、一度設定した辞書を未来永劫変えてはならないものであろうか。多分、そんなことはない。
恐らく、人間の場合でも不変ではないと想像される。
文字認識装置でも、開発担当者は、顧客から苦情が来る度に辞書の改良を重ねて、
残業の連続になることも稀ではない。
したがって、ある時点で0 (ゼロ) と認識されていたパターンが、
辞書の改良 (改悪) によって6 (ロク) と認識されることはあり得る。
したがって、次の結論が導ける。
「クラスを固定した場合、標準パターンを変化させることを許容すれば、
時間が経過するとクラス境界が変動することがある。」
3.3 クラス増加
次に、認識対象クラスを増した場合、例えば数字から英数字に拡張した場合について、
思考実験をやってみよう。
安田理論における安定性(不変則)を満足する認識方式があったとする。
クラスを増加させた瞬間には確かに安定性が成立しているかも知れない。
しかし、前小節で述べたように標準パターンは時間的に変動するものである。
そのため、クラスを増加させた時点で0 (ゼロ) と認識されていたパターンが、
その後の辞書の変化によって、6 (ロク) と認識されることはあり得る。
時間を遡らせて、この辞書の変化が、クラスを増加させた瞬間と同時に起きたと考える。
すると、実は安定性は成立していなかったことになる。
この思考実験の結果から、次の結論が導ける。
「 辞書の時間的変化を許容すれば、パターン認識の不変則は成立しない。」
安田理論では、辞書(標準パターン)が時間的に変動するものであることを見落している。
本 3.3 節の議論は安田理論の仮定2.を無視しているから批判になっていない、
という反論は成立するであろう。本節の議論は今から考えると不要であり、
単純に不変則批判再論を展開した方が良かった。
3.4 飯島のモード関数展開は不変則を満たさないか
[1] において、飯島のモード関数展開は現実問題に全く通用しないと指摘している。
その理由はモード関数展開法が不変則を満足しないためだとしている。
しかし、この批判は飯島のモード関数展開 (K--L展開) の適用の仕方に関係する。
1970年代の私の理解では、飯島理論における学習とは、各クラスから代表パターンを1個選び、
その集合についてK--L展開してパターン空間の主軸を求める、というものであった。
この理解では、クラス数が増加するとK--L展開をやり直すことになるので、
パターン空間の主軸が変化する。確かに、この展開に基づいた辞書は不変則を満たさない。
しかし、5節でニューラルネットワークについて展開したのと同じ学習方法を取れば、
K--L展開を用いて不変則を満足する学習方法がある。
実は議論が逆で、不変則を満足する学習方法は最初に K--L展開について考え付き、
それをニューラルネットワークにも適用したのである。
一方、複合類似度法などで採用されている K--L展開では、
あるクラス内のパターン集合について K--L展開を適用し、
他のクラスについては顧慮しない。したがって、不変則を満たす辞書が得られるのである。
4 対判定について
4.1 何故、対判定か
安田氏は
[不変則の紹介]の式(5)で定義される対判定は不変則を満たし、
その特殊ケースとして類似度法があると指摘している。
この主張は正しく、辞書が時間的に不変であるという前提の下で、対判定法の安定性は成立する。
しかし、対判定ではなく、3判定、4判定、5判定、一般に m判定は安定性条件を満たすのである。
ここで、m判定とは次のように定義される (N ≧ m >0)。
「N個のクラスの全ての個数mの部分集合を考える(NCm 通りある)。
各部分集合で予選勝ち抜き者を選び、
自己の属する部分集合の中で全て 1位となったクラスを優勝者と決める。」
このように定義した m判定は安定性要件を満たす。
一般に m判定の中で、なぜ m=2 に固執するのかが理解できない。
もちろん、これは形式的な議論であって、実用性を考えれば
m=2 (あるいはその特殊な場合である m=1) が最適であるかも知れない。
しかし、ここでの議論は一般原理についてであることを想起しよう。
4.2 何故、類似度法か
安田氏はいわゆる類似度法は対判定の特殊な場合であることを指摘する。
(4.1節の立場では、m判定のうち、m=1 の場合がいわゆる類似度法である。)
したがって類似度法は不変則を満たすから優れていると示唆しているように見える。
しかし、不変則批判再論で述べるように、
m=1 の m判定は類似度法に限らない。任意の認識手法において、
あるクラスの標準パターンを決定するとき他のクラスを顧慮しなければ、
m=1 の m判定になるのである。
たとえば、昔流行したオートマトン型の認識方式でも、
あるクラスのパターンを受理するオートマトンの設計 (これが学習である) において、
他のクラスのことは考えずに設計することは可能であり、そうすれば不変則は満たされる。
5 ニューラルネットワークについて
5.1 ニューラルネットワークにおける相互相関について
[1] におけるニューラルネットワークに関する議論には、安田氏の誤解があると思われる。
[1] に示された、相互相関によって識別関数 (識別超平面)
を定めるという認識方式は昔提案されたことがあると記憶している。
確かに、この方式はクラスを決めて、その中のパターン群から識別関数を決めるので、
クラスが増える度に識別関数を設計し直さなければならず、安定性を満たさない。
だから、その方式はダメだという議論は、論理としては成立する。
しかし、逆伝搬学習による階層型ニューラルネットワークは、
相互相関によって識別関数を決定するわけではない。
したがって、安田氏の所論は、
逆伝搬学習による階層型ニューラルネットワーク一般を攻撃したことにはなっていない。
5.2 ニューラルネットワークは不変則を満たさない
もっと単純に、逆伝搬学習による階層型ニューラルネットワークは安定性を満足しないからダメ、
という主張が成立する。
数字で学習が完成した階層型ニューラルネットワークが存在したとする。
これを英数字に拡張するため、新しいパターンを1個でも食わせて学習すれば、
結合係数が変化するので識別境界は変動し、安定性を満足しないことは明かである。
5.3 ニューラルネットワークは不変則を満たさないか
しかし、5.2 節の攻撃に対して、不変則を満足したニューラルネットワークを作って、
反撃することができる。
最初から英数字で学習したネットワークを作っておき、それを数字サブセットに適用する。
数字だけを認識対象とする場合でも、ネットワークの学習を英数字で行うところがミソである。
そうすると、認識対象を英数字に拡張しても、
このネットワークは不変則を満足した認識方式になっている。
もちろん、この議論には穴があることは承知している。
英数字で学習したネットワークがあったとして、
認識対象を英数字+カタカナに拡張するときはどうするのか、ハングルはどうか、漢字は、
といった攻撃があり得る。理論的には全ての字種に対して最初から学習しておけば良いが、
それが実用的かどうかは疑問がある。しかし、ここでは哲学的な議論を展開しているのである。
5.4 不変則を満たすニューラルネットワークの学習方式(1)
5.2 節で述べたように、逐次的にクラスを増加させて行くとき、
ニューラルネットワークは安定性条件を満たさない。
しかし、不変則を満たす学習方式がある。思考実験を行ってみよう。
数字について学習が完成したネットワークがあったとする。
あるパターンに対し、このネットワークの端子0−9の出力が
0.9、0.2、0.3、0.4、0.5、0.4、 0.7、0.6、0.8、0.6
であったとする。したがって、このパターンは0と認識される。
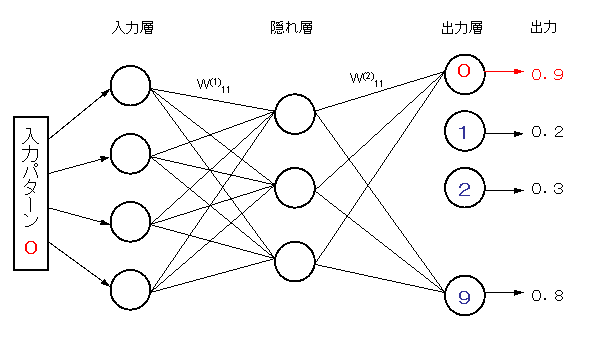
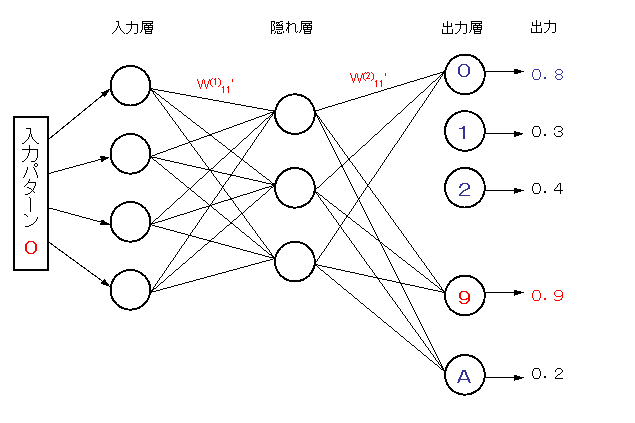
次に、このネットワークに、英字のための出力端子と結合を追加し、英字を加えて学習させる。
その結果、端子0の出力が 0.8、端子8の出力が 0.9、と逆転し、認識結果が8になった。
すなわち、安定性はない。
しかし、ここでこのパターンに対する教師信号として、端子0−9の出力が
0.9、0.2、0.3、0.4、0.5、0.4、0.7、0.6、0.8、0.6 となるように学習させる
(英字に対する教師信号は適当で良い)。
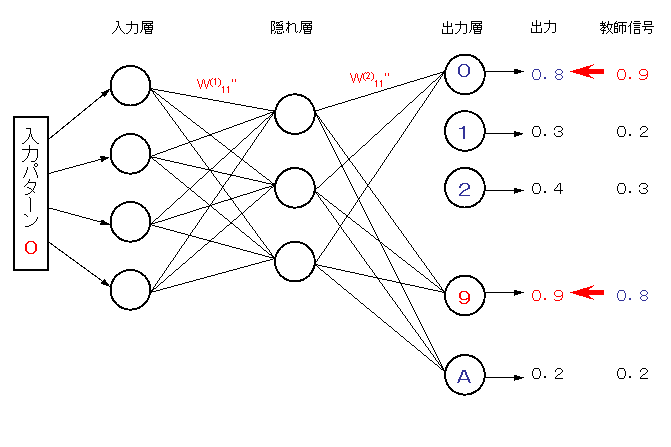
こうすれば、クラス追加を行っても不変則は満たされる。
したがって、次の結論が得られる。
「 逆伝搬学習を用いたニューラルネットワークで、
不変則を満足する学習方式が存在する。」
実は、この結論が成立するためには、ニューラルネットワークの学習が収束しないといけない。
仮に学習が収束するとしても、意味のある時間内に収束するか、という問題は残っている。
しかし、この議論は形式的な議論であることに注意しよう。
5.5 不変則を満たすニューラルネットワークの学習方式(2)
不変則を満たす別の学習方式がある。
数字に対して、ニューラルネットワークを構成し、逆伝搬学習が収束したとする。
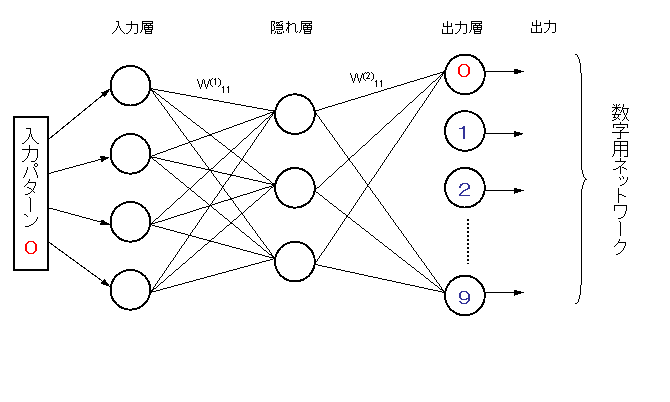
これとは全く別なニューラルネットワークを用意し、英字に対して逆伝搬学習を行って、収束させる。
ただし、入力層の素子数は数字に対するネットワークと等しくする。
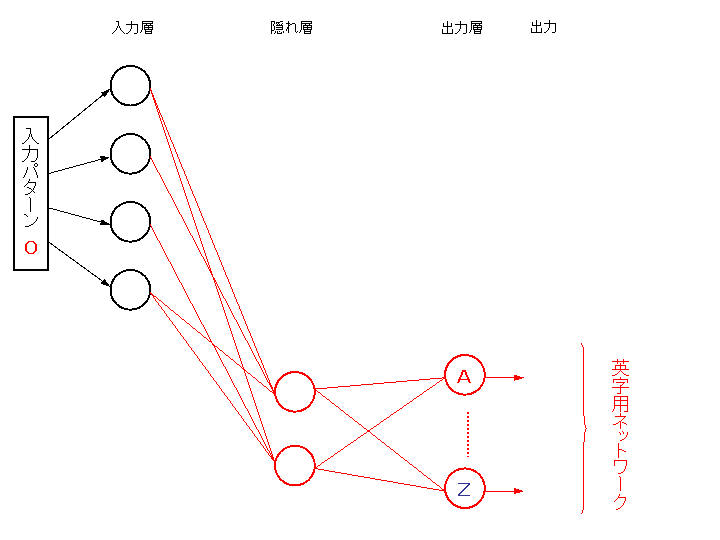
数字から英数字に拡張したとき、この二つのネットワークの入力層を共通結線で結べば、
安定性要請を満足するネットワークが得られることは自明である。
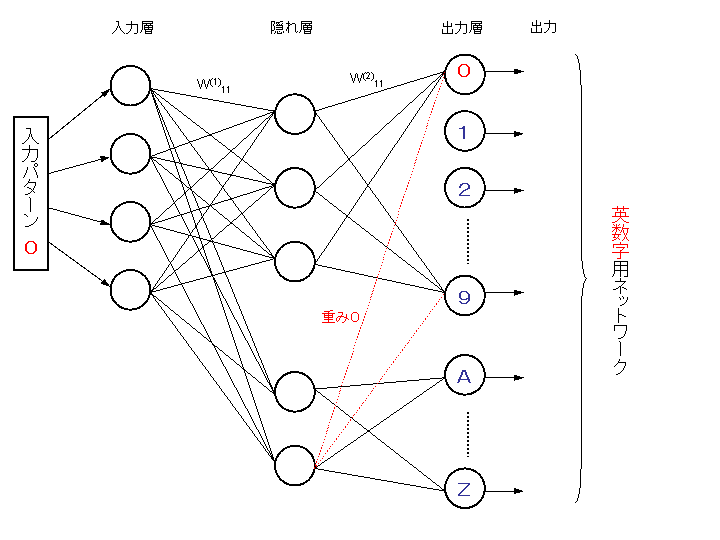
ただし、このネットワークでは、二つの部分ネットワークの層間の結合がないので、
完全結線ネットワークになっていない。この問題は理論的には簡単に解決できる。
結線を追加し、結合加重を0にすれば、完全結線ネットワークになる。
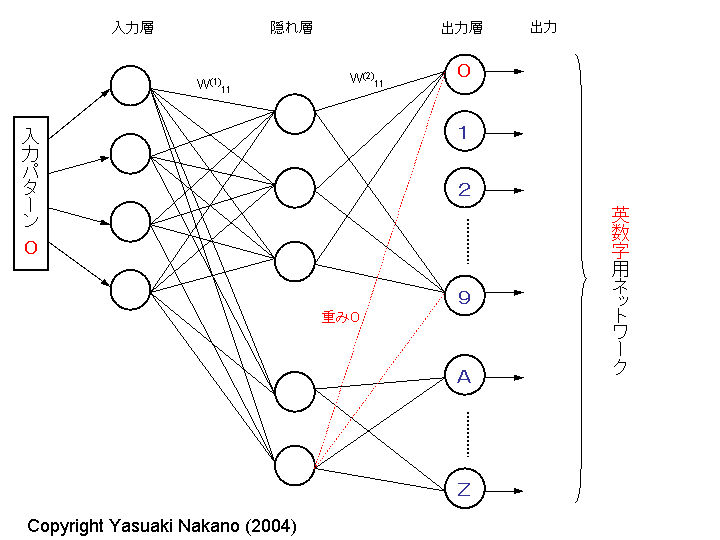
このネットワークは、英数字の類似文字間の分離性能が極めて悪いことは容易に想像でき、
実用性は甚だ疑問であるが、不変則を満たすということが至上命令なら、このようにすれば良い。
(ただし、二段判定を持たないパターン整合法も、同じ弱点を持つ筈である。
対判定擁護参照。)
5.6 不変則を満たすニューラルネットワークの学習方式(3)
本節はつい最近 (2004年) 思いついたものである。
詳細は対判定批判再論に譲るが、
実は、安田理論の仮定2.は不変則と同じことを言っているのに等しい。
「仮定2.のもとで不変則が成立する」というのは、ほとんど同語反復に近い。
5.7 クラス追加時の安定性の保持について
5.5 節で述べた「英数字間の分離性能が極めて悪い」という点を改良するには、
統合した完全結線ネットワークで追加学習を行えば、
完全結線前の結合加重も含めて全体の結合加重が修正され、
認識性能は上昇するであろう。しかし、そうすると統合時点で成立していた不変則が崩れる。
安定性を至上命令と仮定したとき、認識性能向上と安定性要請が両立しないことが、
5.5節で述べた認識方式(学習方式)の欠点であると考えていたが、
実はパターン整合法でも同じことが言えることに気付いた。
話を簡単にするため、単純なパターン整合法で、標準パターンはクラス当り1個である場合を例に取ろう。
数字から英数字に拡張するとする。そのためには、英字に対する標準パターンを追加するだけで良い。
もちろん、その瞬間には安定性要請は満足する。
しかし、英数字では、0−O、8−B、S−5、などの類似文字対があるため、認識率が大きく悪化する。
(この事情はニューラルネットワークと同じである。)
認識率向上のため、標準パターンを修正したり、認識アルゴリズムを改良したりすると、
その時点で安定性が破壊される。
これらの対策は本小節のニューラルネットワークと同じディレンマを抱えるのである。
唯一取り得る対策は、二段判定の採用、すなわち類似文字弁別のための専用アルゴリズムの追加であろう。
これならば、一段判定(パターン整合法)の結果に基いているので、安定性要請を満たすように思われる。
しかし、二段判定が常に正しく判定する保証はないので、結局のところ安定性要請は満されない。
二段判定については「二段判定と検定」を参照されたい。
具体例を挙げないと理解しにくいので、仮想例を示す。
一段判定(類似度での評価)での順位が、5−S−6だったとする。
数字モードでは類似度の大小だけで決めて良いとすれば、認識結果は5である。
英数字モードでは、三者の間の類似度差が小さくて、二段判定に持ち込まれたとする。
これが正しく行われる保証はなく、たとえば5−Sの対決でSが勝ち、
5−6、6−Sの対決で6が勝ったとすると、認識結果は6である。
つまり、安定性は保持されない。
一段判定を覆すような二段判定を認めないとすれば、安定性要件は満足される。
しかし、それでは何故二段判定を持ち込むかという理由付けができない。
やはり、認識性能向上と安定性要請の両立というディレンマを解決できない。
5.8 ニューラルネットワークによる認識と不変則
第5章の結論をまとめる。
「 逆伝搬学習を用いたニューラルネットワークでも、
不変則を満たす学習方式が存在する。」
6 結論
6.1 反論のまとめ
安田理論 [1] に対する反論を行い、次のことを示した。
- 辞書の時間的変化を許容すれば、パターン認識の不変則は成立しない
- 逆伝搬学習を用いたニューラルネットワークでも、不変則を満たす学習方式が存在する
参考文献
[1] 安田道夫,パターン認識における不変則, (京都大学数理解析研究所, Nov. 1996):
概要を不変則の紹介に示す。
[不変則の紹介]
[不変則批判]
[不変則批判再論]
[対判定擁護]
←[パターン認識雑論]
←[中野の研究紹介]
←[中野の目次]
| mail address: |
 |
← お手数ですが打ち込んで下さい |
First Written June 19, 2004
Transplanted to So-net May 3, 2005
Last Update April 22, 2007
© Yasuaki Nakano 2004-2007








