対判定擁護
[不変則の紹介]
[不変則批判]
[不変則批判再論]
[対判定擁護]
←[パターン認識雑論]
←[中野の研究紹介]
←[中野の目次]
対判定擁護:対判定と二段判定について
1. はじめに
「不変則は対判定の本来の可能性をつぶしているのではないだろうか」という議論がある。
この点は不変則批判の第5.6節に関係するので、
本ページで解説する。
対判定に関する解説は安田氏の資料 [1]には詳細には書いてない。
本ページの内容は、
昔あるところで安田氏の書かれた非公開報告の内容を私の記憶で復元・増補したもので、
私の独創ではない。
公開文献では、全国大会予稿(?)で安田氏が発表されていたと思う。
2. 二段判定と対判定
最初に、二段判定と対判定を区別する。
2.1 二段判定
Sと5の区別のように、通常教科書に載っているパターン整合法あるいは構造解析法では、
類似文字の区別は困難なことが良くある。
このような場合、如何に辞書やパラメータをいじって見ても、弁別は困難なことが多い。
したがって、実用上は二段判定(ズーミング)が必要となる。
二段判定とは「S−5」のような類似クラス対だけに特化した認識手法をいう。
この場合、常用手書きなら左下のセリフの有無を見る処理、自由手書きなら、
左肩の曲率の大小を判定する処理になるだろう。
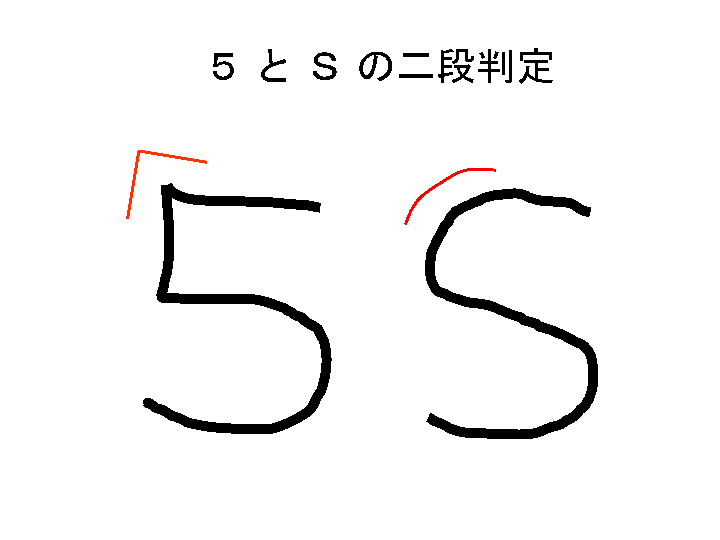
自由手書き文字の「S−5」の弁別は左肩の曲率の大小を判定すれば良いだろう。
全クラスを対象とした汎用処理を一段判定と呼び、二段判定と区別する。
音声学の用語を借りれば、
二段判定とは二つのクラスの間の示差特徴(distinctive features)を抽出し、
入力パターンがそのどちらに属するかを判定する処理である。
2.2 対判定とトーナメント方式
対判定という言葉は、この二段判定を意味していると取られる可能性がある。
すると、不変則によって対判定(二段判定)の自由度が殺されるという印象を与えるかも知れない。
しかし、安田氏のいう対判定は二段判定とは必ずしも等価ではない。
対判定によるパターン認識方式は、次のようなものである。
数字に例を取る。
あらゆる二つのクラスの組み合わせ、「0−1」、「0−2」、・・・、「0−9」、
「1−2」、・・・、「1−9」、「2−3」、・・・・、「8−9」の間で、
どちらが勝つかを判定する手続き(10C2=45通り)を用意する。
そしてトーナメント方式で、各試合でどちらが勝つかを決める。
1回戦で勝ち上がった同士で勝負する。どこが勝とうとも、
勝ちクラス同士の対判定は用意されているので、2回戦の勝敗は決まる。
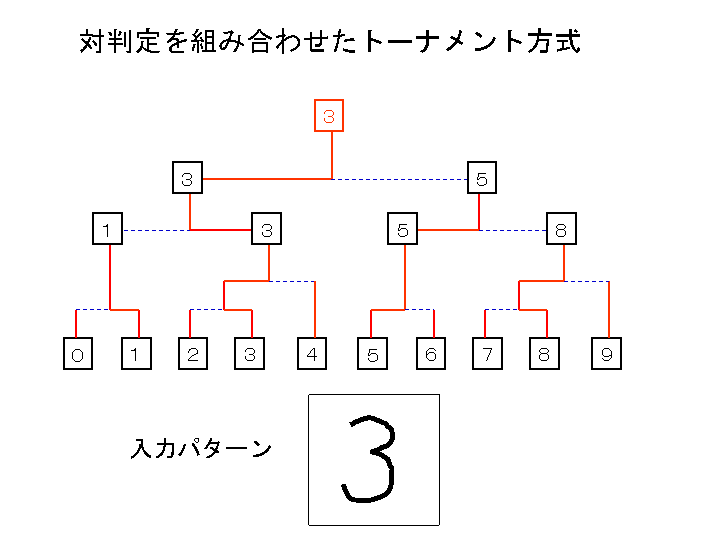
以下同様に進め、最後に1クラスが勝ち残るまで続ける。
優勝したクラスと、対戦していない全てのクラスとの間で対判定を行い、
確かに他のどのクラスにも勝つことが確認できれば、これを認識結果とする。
トーナメント方式でなくて、リーグ戦方式でも構わない。ただし、試合数が増加するので不利である。
クラス数を N とするとき、リーグ戦方式だと、
必要な対判定の実行回数は、NC2=N (N-1) / 2回である。
一方、「トーナメント+確認」方式の場合、 (2N - 1 - log2 N)回で済む。
2.3 対判定に関する諸注意
簡単のため、引き分け=リジェクトはないものとするが、あっても問題ない。
三すくみ状態があると、トーナメントの組み合わせによっては、
本来は負ける筈の候補が優勝することがないか心配になるかも知れないが、問題ない。
確認のための対戦を入れることで解決している。
一見、対判定方式は奇妙である。
入力パターンが3であったとき、これに「0−1」の対判定を適用すると、
とんでもない結果にならないか、心配になるもしれない。
しかし、この対判定でどちらが勝とうとも、いずれ「0−3」または「1−3」の勝負が行われ、
3が勝つであろうから、問題ない。
3 対判定は不変則を満たす
この認識方式は、安田理論でいう不変則を満足する。
3.1 クラス増加時の状況の説明
認識対象クラスを数字から英数字に増加したとき、どのような対判定を追加すべきであろうか。
答えは、A−Zの英字同士の対判定と、
英字対数字の「1−A」、「1−B」、・・・、「1−Z」、・・・、「9−Z」、である
(対判定の総数は 45 から 36C2= 630 に増加する)。
この対判定を加えて、トーナメント方式(リーグ戦方式)を行ったとする。
数字モードで5と判定されていたパターンは、Sには負けるかも知れないが、6に負けることはない。
6のみならず、数字には絶対に負けない。
したがって、不変則は満たされる。
4 不変則は対判定の可能性を殺すか
4.1 形式的議論
不変則が対判定の可能性を殺すことはない。
S−5の対判定は、対象クラスが数字のときは考える必要がない。
つまり、対象クラスを英数字に拡張した時点で考えれば良いことである。
したがって、クラスを拡張した時点で、
数字の範囲での5の標準パターンに影響を与える必要がないのである。
ここで、5の標準パターンとは、5と他の数字との対判定の集合を意味する。
4.2 対判定と二段判定
ところで、対判定として、どのような処理を行ったら良いだろうか。
類似文字の場合「二段判定と一致する」であろう。
つまり、「5−S」なら、その間を最も良く弁別する特徴を見るべきであるからである。
しかし、二段判定は、全く似ていない文字同士では組む必要がないのに対し、
対判定は(似ていようが、いまいが)全ての対に対して用意しておかねばならない点が異なる。
5 でも、ちょっと変だな
でも、何となくだまされたような気分になった人もいるかも知れない。
それは、次の二つの方式を混同しているからであろう。
- (1) 一段判定でパターン整合法を用い、近接リジェクトのとき二段判定を使う
- (2) 全クラス同士の間に対判定を用意しトーナメント法 (+確認) で認識する
ここで (1) の二段判定と (2) の対判定は同一のものとする。
そのとき、方式 (2) は不変則を満足するが、方式 (1) は必ずしもそうでない。
その理由は不変則批判の第5.7節を見られたい。
参考文献
[1] 安田道夫,パターン認識における不変則, (京都大学数理解析研究所, Nov. 1996):
概要を不変則の紹介に示す。
[不変則の紹介]
[不変則批判]
[不変則批判再論]
[対判定擁護]
←[パターン認識雑論]
←[中野の研究紹介]
←[中野の目次]
| mail address: |
 |
← お手数ですが打ち込んで下さい |
First Written June 19, 2004
Transplanted to So-net May 3, 2005
Last Update April 22, 2007
© Yasuaki Nakano 2004-2007



