図では各クラスの領域は離れているが、隣接していても構わない。 場合によっては重なっていても良いが、 入力パターンの特徴が重複領域に落ちたときは近接リジェクトになる。
学習とは、標準パターンの設定方法と言い替えることができる。
非常に単純なパターン整合法では、 標準パターンとして、あるクラスを代表するパターンそのものを使うことがある。 これから、標準パターンの表し方はパターンそのものであると誤解されることがある。
しかし、標準パターンは、整合法に限らず、任意の認識方式に存在するものである。
[方式1]
例えば、あるパターンの二つの特徴パラメータが、
平面上でどこに落ちるかでパターン認識を行うものがある。
(実際には特徴は多次元であることが多いが、話としては同じである。)
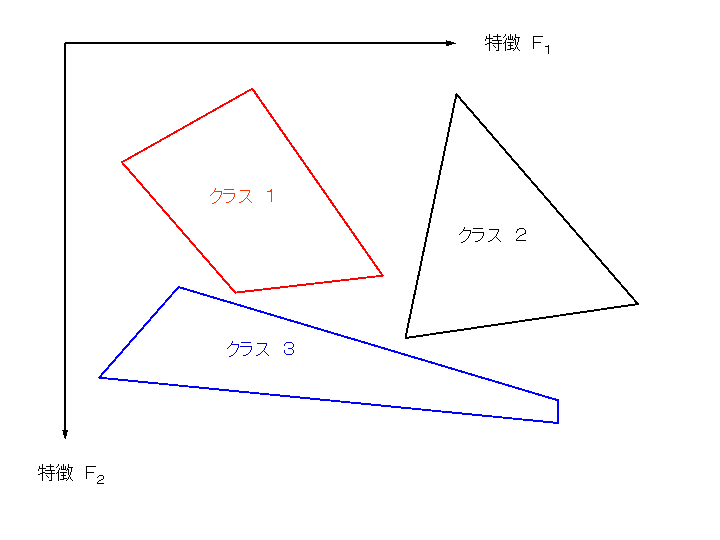
平面をいくつかの領域に切って、どの領域に落ちるかで判定するのであるが、
その切った領域が標準パターンである。

図では各クラスの領域は離れているが、隣接していても構わない。
場合によっては重なっていても良いが、
入力パターンの特徴が重複領域に落ちたときは近接リジェクトになる。
[方式2]
ある特徴について、クラスごとにその特徴パラメータの受理範囲 (最小値と最大値) を決め、
全ての特徴について特徴パラメータがあるクラスの受理範囲に入れば、
そのクラスであるとする判定方式もある。
このときは、受理範囲がそのクラスの標準パターンである。
これは方式1の領域を長方形 (超直方体) とした場合に相当する。
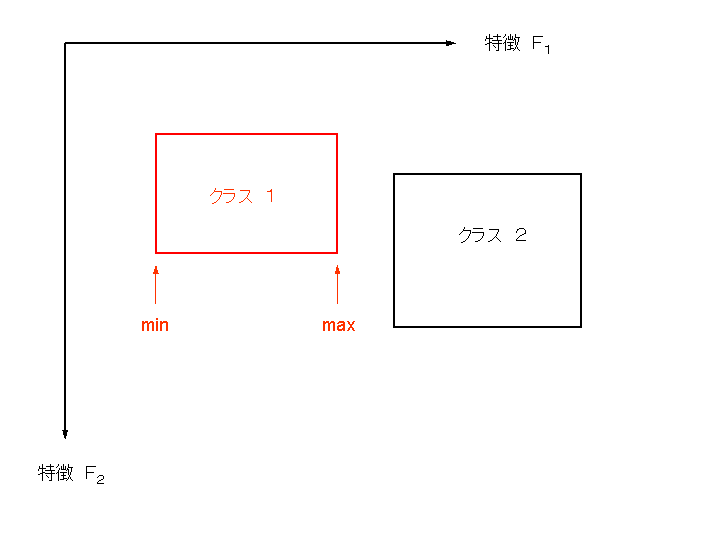
この場合も、各クラスの領域は隣接していても重なっていても構わない。
[方式3]
オートマトン型の認識方式では、
一つのクラスを受理するオートマトンが一つの標準パターンである。
実際にはコストその他の関係で、
複数クラスに対応するオートマトンを1個にまとめてしまう場合もあるが、
このオートマトンをクラスごとのオートマトンに分離することは可能であり、
原理的には1クラス、1オートマトンと見なせる。
学習とは、設計者が多数のパターンを見て、オートマトンの状態数を変えたり、
枝を付けたり外したりする操作がそれに当たる
(性能はともかく、オートマトンを自動学習で構成することも可能である)。
[方式4]
最近いろいろな研究が発表されている HMM (Hidden Markov Model) は、
確率オートマトンの近代化といった印象を受ける。
ある学習パターンを受理する HMM を複数まとめて、
クラス当り1個の HMM を作るものであり、作られた HMM が標準パターンである。
[方式5]
対判定方式では、
あるクラスを一方とする全ての対判定の集合が、そのクラスの標準パターンになる。
この意見が出て来る理由は、
認識手法の良否は認識方式 (認識アルゴリズム) と標準パターン (辞書) の二つで決る、
という事実であると思う。
ドヂな方式であっても、クラス当りの標準パターンを増やせば認識率は上昇する。
したがって、提案した方式の真の実力を見るには、
標準パターンがクラス当り1個という条件で他方式と比較してくれ、という訳である。
しかし、この意見は方式比較の条件と、 その方式によるパターン認識装置の実装とを混同していると思われる。 優れた方式であっても、 実装に際しては認識率を上げるため標準パターンを増加することは広く行われる。 標準パターンの個数と認識率 (認識不良率) の関係については 藤澤の経験則を参照されたい。
標準パターン●から等距離にあれば ○のクラスであると認識する方式を考える。
[標準パターンが1個で良い場合]
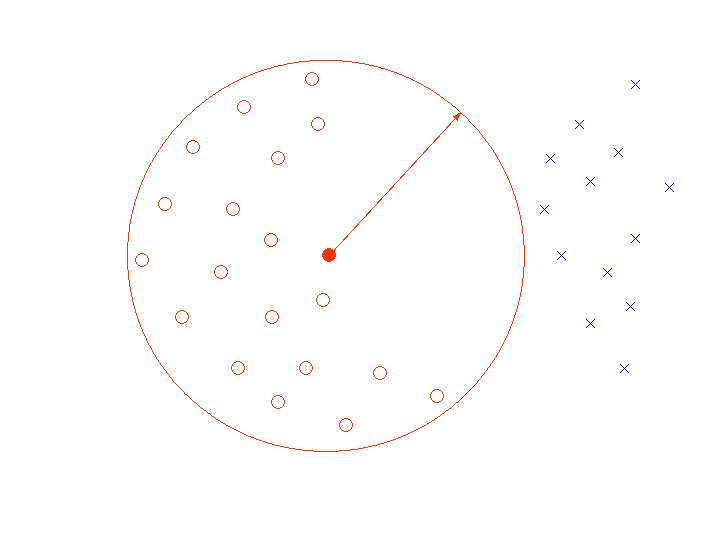
この例のようにパターンが分布していれば、 ×のクラスを○と誤認識することはない。
[標準パターン1個では失敗する場合]
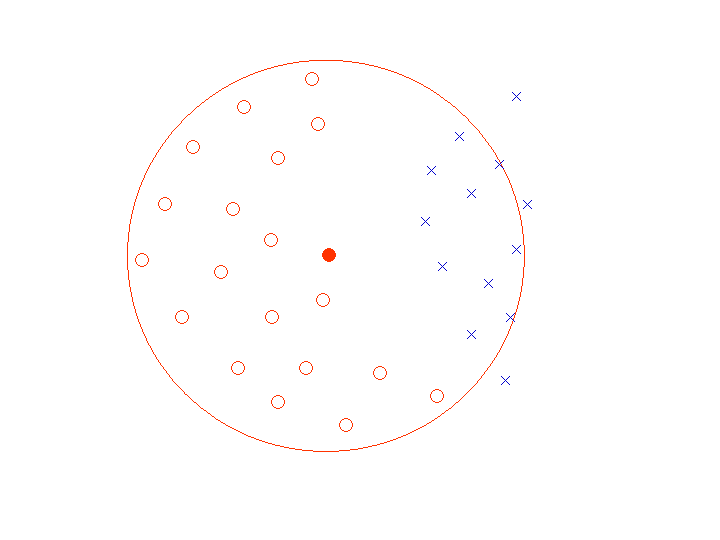
この例のようにパターンが分布している限り、
×のクラスを
○と誤認識することは避けられない。
標準パターン●をずっと左の方に取っても、
全ての○を覆うような円 (超球) を作ると、
×のパターンを捕らえてしまう。
[標準パターン複数化による解]

上記の例でも、標準パターンを複数にすれば誤認識はなくなる。
この仮想例に対しても反論は成立するであろう。
[方向面パターン整合法]
現在では標準的な文字認識方式である
方向面パターン整合法が提案されたとき、
筆者は次のような意見を述べた記憶がある。
この方式は標準パターンとして方向面を4個使うから、
通常の整合法に比べてデータ量が4倍になる。
通常の整合法でクラス当り4個の標準パターンを使用するのとデータ量では同じ
であり、データ量を揃えて従来法と認識率を比較しなくては公平ではない。
[複合類似度法]
複合類似度法では、
あるクラスに属する学習サンプルの集合をK--L 展開し、
展開して得た基底の上位N個を用いて未知サンプルとの複合類似度を計算する。
この場合、標準パターンがクラス当り1個 (一組) というのか、
N個というのか、筆者には良く判らない。
[個数を定めにくい方式]
1. で述べた、方式2:「特徴パラメータの受理範囲」、方式3:「オートマトン」、
方式4: HMM の場合は、標準パターンが何個なのか判然としない。
一組と言えば正確だが、1個だというと抵抗があるだろう。
「特徴パラメータの受理範囲」の場合は、各特徴の中央値を取るパターンを仮想的に考え、
これがクラス (あるいはサブクラス) 当り1個の標準パターンだ、
と主張することも不可能ではない。
極端な場合であるが、手書き漢字認識で「働」を「仂」と書く人がいる。
(実際には「仂」は第二水準の別漢字である。)
表示しにくいが、「第」を「オ」のような字形で書く人もいる。
しかし、「働」でも「仂」でも、認識結果は「働」のコードを出さないといけない。
この二つの字形を同じ1個の標準パターンで認識するのは困難であろう。
オートマトン方式では可能かも知れないが、できたとすれば、最初の段階で枝別れさせ、
実際には二つのオートマトンを合併したものであるだろう。
「働」と「仂」ほど変形が極端でなくとも、一つのクラスの中で、 どこまでを一つのサブクラスとし、それ以上の変形は別のクラスとするか、は非常に難しい。 技術的にはクラスタリングの応用であるが、完全には解かれていない問題である。
実際問題として、明らかに複数のサブクラスがある場合、 クラス当りの標準パターン1個に固執していては認識率は上がらない。
異なった文字クラス (文字概念) には、異なった文字コードを割り当てる必要がある。 問題は、何をもって異なった文字クラスというかである。
JIS では、「青」の下の旁が「月」か「円」かは僅かな違いである、 として一つの文字概念に包摂してしまっている。 しかし、「干−于」や「己−已−巳」のように、字形の違いは極く僅かでも、 歴史的に別の文字概念である場合は別コードにしている。
「こけら落し」の「こけら (UNICODE 676E)」の漢字は「柿」に似ているが、
別の文字概念である。旁は「市」ではなく「沛」の旁であり、画数が違う。
JIS では「こけら」のコードは付与しないことにしてしまった。
使用頻度が小さいからであろう。
それは仕方がないとして、「肺」の旁まで「市」に変えることはない。
別の文字概念なのに、字形がほんの僅かしか違わない、というのは文字認識の立場からも困る。 「干−于」は「はね」の有無で区別される。 しかし「木」では、縦棒の下に「はね」があってもなくても同じ文字概念である。
UNICODE では、文字クラスとフォント (字形変形) の間にグリフという概念を設け、
異なるグリフに対しては異なったコードを付与することにし、
フォントの違いは同じグリフに包摂することにした。
しかし、どこまでフォントが異なっても同じグリフに包摂するか、
という基準がない上に、そもそもグリフの明確な定義がない、とする論者もいる。
日本漢字の「骨」と中国漢字の「骨」では、パターンは左右鏡像関係にあるが、
UNICODE では同じグリフ (したがって同じ文字クラス) に包摂している。
これは非常に判りやすい例なので良く取り上げられる。
この人に言わせると「応用数学には、巡回セールスマン問題のようにパラメータをNとすると、
手数がN!のオーダになる問題が多数ある。しかし、パターン認識は1のオーダの問題である」
のだそうだ。
文字に例を取れば、文字パターンをメッシュ数H×Vで表現し、
各画素の取る値を“1,0”とすれば、
異なったパターンの種類は2H×V通りで有限である。
2H×Vバイトのメモリを設け、
各パターンの文字コードを対応するアドレスの内容として書いておけば、
どんなパターンが入って来てもアクセス1回で文字コードが出力できる。
実際には、文字パターンの標本化メッシュを20×20くらいに小さくしても、
メモリサイズは天文学的だし、
各パターンに文字コードを打ち込んで行く時間は宇宙創生から始めたとしても完成にはほど遠い。
実際上は役に立たない解決策である。 しかし、仮に上記のようなメモリができたとすれば、認識率は非常に高いであろう。
ときどき、パターン認識分野で、自分の提案した手法では学習セットに対する認識率を示し、 従来手法より認識率が高いと主張する論文を見かける。 よく調べると、従来手法の認識率は検査セットに対するものだったりする。
3.1 節の手法に近いが、学習セットでは認識率100%にする方法がある。
学習セットの全てのサンプルそのものを標準パターンとして覚えておけば良いのである。
学習セットでは認識率100%になることは明らかである。
標準パターン数は極めて多くなる。検査セットに対する認識率は惨憺たるものであろうが、
少くとも誤認識はない。
[標準パターンとは何か]
[Nagy の法則]
["R+10E" 基準]
[藤澤の経験式]
←[パターン認識雑論]
←[中野の研究紹介]
←[中野の目次]
| mail address: |  |
← お手数ですが打ち込んで下さい |
First Written June 19, 2004
Transplanted to So-net May 3, 2005
Last Update April 22, 2007
© Yasuaki Nakano 2004-2007